Exploring Bayes Point Machine with Infer.NET

Infer.NET is a framework developed by Microsoft research for running Bayesian inference in graphical models and for probabilistic programming. Along with tutorials and examples, Infer.NET 2.4 beta 2 which was recently made avaialble (17th Dec 2010) can be downloaded from here.

In this example we explore the similar concept as described in the infer.net bayes point machine tutorial however this time we will try it out with the weather dataset. The complete code of this example can be downloaded from the link at the bottom of this post.

Our dataset was nominally represented as follows which was converted to it's ordinal form for ease of calculation.

@attribute outlook {sunny, overcast, rainy}
@attribute temperature {hot, mild, cool}
@attribute humidity {high, normal}
@attribute windy {TRUE, FALSE}
attribute play {yes, no}
@attribute outlook {sunny, overcast, rainy}@attribute temperature {hot, mild, cool}@attribute humidity {high, normal}@attribute windy {TRUE, FALSE}@attribute play {yes, no}

Let's visit the important sections of the code; first the usual includes. These namespaces are required for running the inference engine using Infer.NET

using System;
using MicrosoftResearch.Infer;
using MicrosoftResearch.Infer.Distributions;
using MicrosoftResearch.Infer.Maths;
using MicrosoftResearch.Infer.Models;

Next is the initialization of the dataset.

double[] outlook = {0, 0, 1, 2, 2, 2, 1, 0, 0, 2, 0, 1, 1, 2};
double[] temperature = {0, 0, 0, 1, 2, 2, 2, 1, 2, 1, 1, 1, 0, 1};
double[] humidity = {2, 2, 2, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1, 2};
double[] windy = {0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1};
bool[] play = {false, false, true, true, true, false, true, false, true, true, true, true, true, false};

and this is where we create a target variable y to predict the playability.

VariableArray y = Variable.Observed(play).Named("y");

After initializing the random variable to reflect the dimensions of the input data, we initialize a Bayes point machine with the given dataset.

Variable w = Variable.Random(new VectorGaussian(Vector.Zero(5),
PositiveDefiniteMatrix.Identity(5))).Named("w");
BayesPointMachine(outlook, temperature, humidity, windy, w, y);

The code for how BayesPointMachine is constructed can be seen in the enclosed zip file. And now we are all set to let the inference begin.

var engine = new InferenceEngine();
if (!(engine.Algorithm is GibbsSampling))
{
var wPosterior = engine.Infer(w);
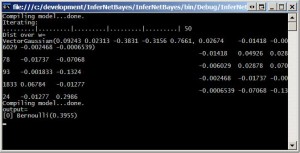
Console.WriteLine("Dist over w=\n" + wPosterior);

Now that model has been complied,  let's initialize a "test" data; we can see that this will result in play happening because the outlook is

double[] outlooktest = {1};
double[] temperaturetest = {0};
double[] humiditytest = {2};
double[] windytest = {0};

variableArray ytest = Variable.Array(new Range(temperaturetest.Length)).Named("ytest");
BayesPointMachine(outlooktest, temperaturetest, humiditytest, windytest,
Variable.Random(wPosterior).Named("w"), ytest);
Console.WriteLine("output=\n" + engine.Infer(ytest));

Upon running this test, we find that the, probability of play is approaching 0.6 which means there is a higher chance of a play.

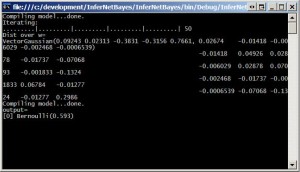
However, if you run it with a different test set, the probability results in no play i.e. 0.3995.

double[] outlooktest = {2};
double[] temperaturetest = {1};
double[] humiditytest = {2};
double[] windytest = {1};

The Bayes point machine gets initialized and runs as follows.

public static void BayesPointMachine(double[] outlook, double[] temperature, double[] humidity, double[] windy, Variable w, VariableArray y)
{
// Create x vector, augmented by 1
Range j = y.Range.Named("play");
var xdata = new Vector[outlook.Length];
for (int i = 0; i < xdata.Length; i++)
xdata[i] = Vector.FromArray(outlook[i], temperature[i], humidity[i], windy[i], 1);
VariableArray x = Variable.Observed(xdata, j).Named("x");
// Bayes Point Machine
double noise = 0.1;
y[j] = Variable.GaussianFromMeanAndVariance(Variable.InnerProduct(w, x[j]).Named("innerProduct"), noise) > 0;

}

The code and dataset can be downloaded from here

InferNetBayes Example with Weather Nominal Data

Happy Inferencing!

References:
Bayes Point Machines MSR