Even though Kurtz and Simon proved that a natural generalization of the Collatz problem is algorithmically undecidable, it is still fairly easy to brute force the 3n+1 conjecture with large values of n and empirically see it converge. Project Euler's problem 14 queries about which starting number, under one million, produces the longest sequence?
Since Premature optimization is often considered root of all evil, a brute force way to approach this problem would be as simple as follows.
private static void CollatzSequence (ulong max)
{
ulong startingNum = 0;
ulong longestSequence = 0;
for (ulong i = 1; i < max; i++)
{
ulong member = i;
ulong sequenceCnt = 0;
while (member != 1)
{
if (member%2 == 0)
member = member/2;
else
member = 3*member + 1;
sequenceCnt++;
}
if (longestSequence < sequenceCnt)
{
longestSequence = sequenceCnt;
startingNum = i;
}
}
Console.WriteLine("Sequence Starter:" + startingNum + " - Longest Sequence=" + longestSequence);
}
The core of the algorithm is within the convergence test stated below
while (member != 1)
{
if (member%2 == 0)
member = member/2;
else
member = 3*member + 1;
sequenceCnt++;
}
This executes in 5601.2944 ms or approx 5.6 seconds resulting in starting element to be 83779 with the longest sequence 524 elements. Not bad but this can definitely be optimized.
By looking at the pattern of sequence generated, it's clear that there is constant repetition or cycle which occurs within the sequence before converging to 1. Therefore, if we can break down this execution into segments by storing the length of repeated cycles, these segments can then be "appended" later to count the total steps in the convergence path. This is essentially the application of dynamic programming which is a very powerful algorithmic paradigm. In DP, a problem is solved by identifying a collection of sub problems (segments) and handling them one by one, smallest first, using the answers to small problems to help figure out larger ones. Some good dynamic programming problems can be found here.
In order to record and retrieve the earlier steps as segments, I decided to use a simple hashtable. This hashtable will store an element in sequence as a key and the count of elements in the path as value. Therefore, whenever a familiar recurrence happen, we can easily find the segment and stop the processing to move on.
if (dynPrg.ContainsKey(member))
{
sequenceCnt += ulong.Parse(dynPrg[member].ToString());
member = 1;
}
By using this approach, we get the same results in about 4 seconds however there is a time-space trade-off. There are approx 91K entries in the hashtable now; Hashtable can be pruned for further optimization. The complete listing follows.
private static void CollatzSequenceDP(ulong max)
{
ulong startingNum = 0;
ulong longestSequence = 0;
var dynPrg = new Hashtable();
for (ulong i = 1; i < max; i++)
{
ulong member = i;
ulong sequenceCnt = 0;
ulong firstterm = 0;
while (member != 1)
{
if (member % 2 == 0)
member = member / 2;
else
member = 3 * member + 1;
if (firstterm == 0)
firstterm = member;
if (dynPrg.ContainsKey(member))
{
sequenceCnt += ulong.Parse(dynPrg[member].ToString());
member = 1;
}
sequenceCnt++;
}
if (longestSequence < sequenceCnt)
{
longestSequence = sequenceCnt;
startingNum = i;
}
if (!dynPrg.ContainsKey(firstterm))
dynPrg.Add(firstterm, sequenceCnt-1);
}
Console.WriteLine("Sequence Starter:" + startingNum + " - Longest Sequence=" + longestSequence + " " + dynPrg.Count);
}
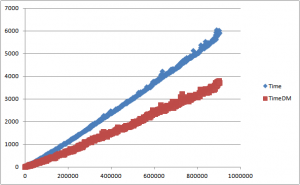
Comparing the results of regular execution and one with dynamic programming approach, we see in the graph below that DM easily out performs unoptimized brute force in time as the execution path gets longer. Following graph is plotted with over 1000 data points for values of n ranging from 10-1000000 step 1000.
Further improvements include parallelization of the algorithm and introducing prime sieves. I will be revisiting it with the Parallel.For construct.
Last but not least, speaking of Dynamic Programming, let's not confuse this with term with computer programming. The term was chosen by Richard Bellmen, the inventor of paradigm to describe schedule. The idea has its roots in mathematics and is a general technique for solving complex optimization problems which can be decomposed into smaller overlapping sub problems.

Comments are closed.