As statistician Dennis Lindley famously said, "Inside every nonBayesian there is a Bayesian struggling to get out"; it would be safe to interpolate that Sharon McGrayne's interesting tale of trials and triumph of the Bayes Rule, or more accurately Bayes-Laplace-Price rule, is an excellent historical journey, which may help get your Bayesian out of the closet.
The Theory That Would Not Die: How Bayes' Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy makes for an interesting and captivating read especially considering that writing about history of mathematics and statistics for general audience is a daunting task when compared with relatively popular topics like astronomy or physics. In this easy reading for popular-science audience, author covers over three hundred years of the history behind Bayes rule with its applications and engrossing stories of mathematical luminaries; some of which thought it was a brilliant way to model real-life scenarios while others considered it unscientific, an exercise in futility and vehemently fought against the idea of incorporating prior beliefs. Aside from providing thorough research on the subject matter, this text also delves into significant details about life and works of important scientists, mathematicians and statisticians including but not limited to Turing, Von Neumann, Price, Shannon, Bailey, Laplace, Fisher and Feynman. Regarding modern times, I was delighted to see Daphne Koller and Heckerman's work mentioned as well as the role Bayesian techniques played in contemporary discipline of Machine learning.
Starting with the compelling statement
When the facts change, I change my opinion. What do you do, sir?
—John Maynard Keynes
the ups and downs of adoption of Bayesian rule are listed as different eras and separated out as different parts of the book. The 17 chapters are divided into five parts namely Enlightenment and the anti-Bayesian reaction, Second World War era, the glorious revival, to prove it's worth and finally, victory. Did author do a good job explaining Bayes rule is the point of contention among earlier reviews. I agree that a few more concrete examples with algebraic expressions may have helped better explaining how Bayesian priors and it's mathematical formulation by early luminaries in the field makes it easy to work without complex integrals. However, it is to be noted that this book is not a course in antiquity of causality and inference but rather a study of Bayesian thought through centuries and it's profound impact on science and technology. The book very well covers the advances by 'Bayesian revolution' in variety of fields including medical diagnosis, ecology, geology, computer science, artificial intelligence, machine learning, genetics, astrophysics, archaeology, education performance, sports modeling, and more.
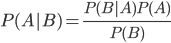
Sharon McGrayne's has picked a very relevant topic for contemporary audience interested in mathematical and computational sciences; making this ~350 page book a very informative, absorbing and pleasurable reading. Although light on technical details, proofs, mathematical equations and problems, this book delivers what it sets to accomplish, to tell the story of Bayes theory. "The theory that would not die" tells the story of a robust idea which is simple, intuitive, unsettling to establishment and yet so resilient that despite of all the criticisms from mainstream frequentists, it stayed alive and well. To quote from the book
"Bayes is still young. Probability did not have any mathematics in it until 1700. Bayes grew up in data- poor and computationally poor circumstances. It hasn't settled down yet. We can give it time. We're just starting."

