"I'm not an outlier; I just haven't found my distribution yet!" -Ronan Conroy
Infer.NET is a .NET library for machine learning which provides state-of-the-art algorithms for probabilistic inference from data. Due to its capability of seamlessly integrating with the .NET code, I have used this library frequently and wrote about Infer.Net in the past; however, during a recent hunt of looking for a functional dialect for probabilistic programming, I came across Infer.NET Fun dubbed as An F# Library for Probabilistic Programming. Being a first class .NET citizen, it was always possible to call infer.net directly from F# but having a "succinct syntax of F# into an executable modeling language" to enjoy the raw-functional-style of language is always the best.
Infer.NET Fun seems to have come out of this research paper Distribution Transformer Semantics for Bayesian Machine Learning and a resulting Microsoft research report by Johannes Borgström, Andrew D. Gordon, Michael Greenberg, James Margetson, and Jurgen Van Gael, Measure Transformer Semantics for Bayesian Machine Learning, no. MSR-TR-2011-18, July 2011
The project is defined as
Infer.NET Fun turns the simple succinct syntax of F# into an executable modeling language. You can code up the conditional probability distributions of Bayes’ rule using F# array comprehensions with constraints. Write your model in F#. Run it directly to synthesize test datasets and to debug models. Or compile it with the Infer.NET compiler and runtime for efficient statistical inference.
The syntax is very powerful and does every effort to makes functional programmer at home. As an example, let's go with the age-old coin toss problem.
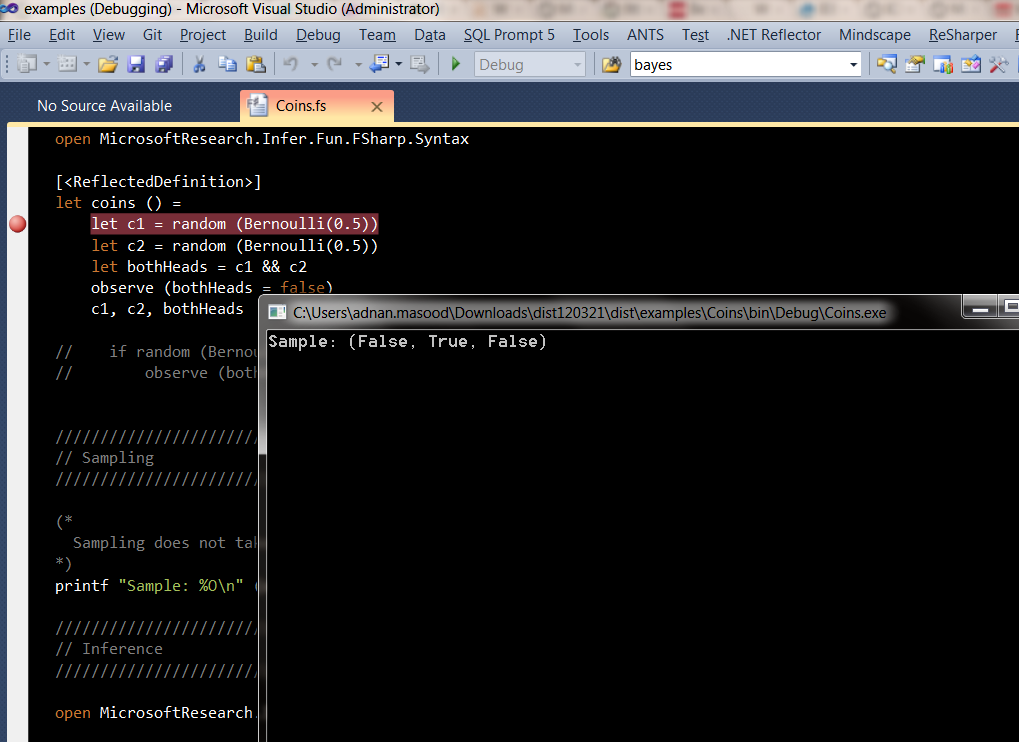
Let's toss two coins and observe that not both of them are heads; now we can use infer,net to calculate the conditional probability that is assigned after the relevant evidence is taken into account. This is called the inference of posterior probability to figure out if each of these were heads. To do so using Infer.NET Fun you start by writing a model as follows:
open MicrosoftResearch.Infer.Fun.FSharp.Syntax
[]
let coins () =
let c1 = random (Bernoulli(0.5))
let c2 = random (Bernoulli(0.5))
let bothHeads = c1 && c2
observe (bothHeads = false)
c1, c2, bothHeads
This is the model definition of the problem. This model is using a function random which returns a random sample from a given distribution. The second function being used is observe which marks the execution as failed if the condition is not satisfied.
It takes some adjustment to be able to understand the functional definition here but the ultimate goal of this inference is to produce the distribution of the output variables of the model across all executions with a condition; no observation should fail (bothHeads=false). Sampling from a model is as simple as calling the function coins(). I am running this in debug mode stepping through as can be seen in the screenshot below.
by printing the output from method, you get the screenshot above for c1, c2 and bothHeads
printf "Sample: %O\n" (coins ())
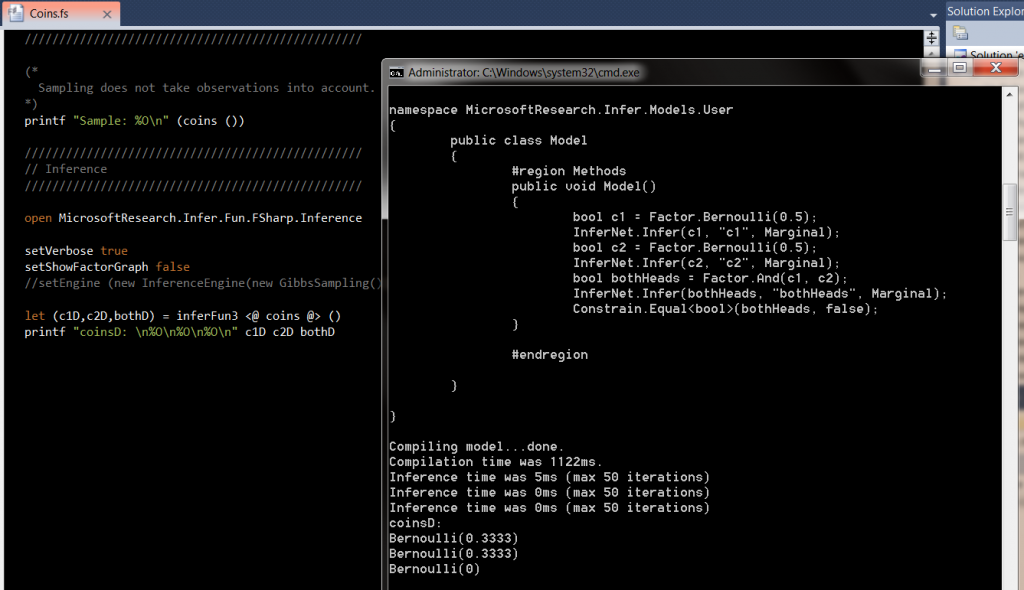
Now, in order to retrieve the model (infer) from the given model which we just setup, you can do the following.
open MicrosoftResearch.Infer.Fun.FSharp.Inference setVerbose true setShowFactorGraph false let (c1D,c2D,bothD) = inferFun3 <@ coins @> () printf "coinsD: \n%O\n%O\n%O\n" c1D c2D bothD
Setting verbosit will be able to demonstrate the underlying model. Now in order to perform inference, the function inferFun3 runs and returns a triple of distributions, one for each return value of coins()
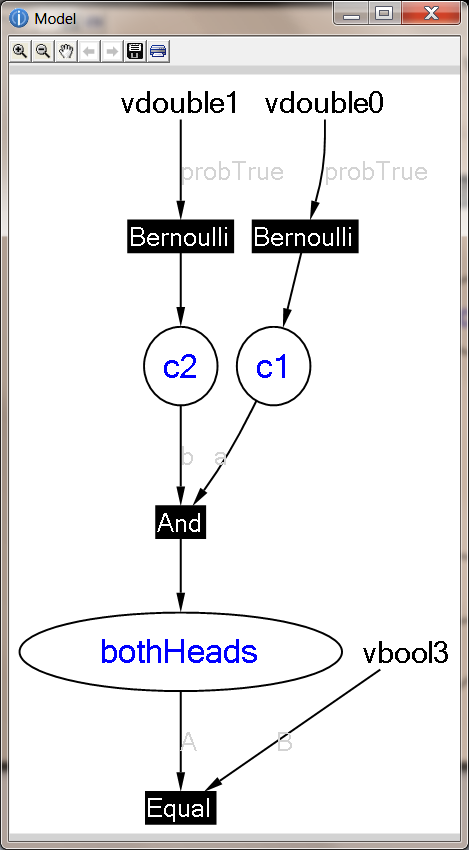
One of the really cool features of infer.net which I like is that by setting the following.
setShowFactorGraph true
The Infer.NET Fun paper concludes with the following information about their contribution. The paper talks about the importance of being able to write probablistic programs directly using a declarative language fun, a subset of F#.
Our direct contribution is a rigorous semantics for a probabilistic programming language that also has an equivalent factor graph semantics. More importantly, the implication of our work for the machine learning community is that probabilistic programs can be written directly within an existing declarative language (Fun—a subset of F#) and compiled down to lower level Bayesian inference engines.
For the programming language community, our new semantics suggests some novel directions for research. What other primitives are possible—non-generative models, inspection of distributions, on-line inference on data streams? Can we provide a semantics for other data structures, especially of probabilistically varying size? Can our semantics be extended to higher-order programs? Can we verify the transformations performed by machine learning compilers such as Infer.NET compiler for Csoft? Are there type systems for avoiding zero probability exceptions, or to ensure that we only generate factor graphs that can be handled by our back-end?
Don Syme have already said that F stands for fun in F# but Infer.NET fun is definitely putting fun in inference and F#, well probably 🙂
Here are the slides and video of the Infer.NET Fun talk at Lang.NEXT 2012.
Reverend Bayes, meet Countess Lovelace: Probabilistic Programming for Machine Learning
Great news for creating probabilistic DSL; as F# is moving into the Enterprise - Accelerated Analytical and Parallel .NET Development with F# 2.0
Happy Infering!